ECUACIONES DIFERENCIALES EXACTAS

 Definición:

Sea la ecuación diferencial:

 Procedimiento:

Ejemplo ilustrativo:

https://youtu.be/dATo9M821ik

LEY DE ENFRIAMIENTO DE NEWTON

 

APRENDIZAJE PERSONAL: 

Aprendimos que debemos saber indentificar el problema ya que los datos ya nos los estan dando, es saber interpretarlos para poder desarrollar la ecuacion y asi poder llegar a la solucion del probelma

APRENDIZAJE COMPLEMENTARIO:

Las ecuaciones diferenciales tienen una gran variedad de usos en las ciencias básicas, uno de los ejemplos de su aplicación se encuentra en la ley de enfriamiento de Newton, en la elaboración del presente artículo se realizó un experimento sobre enfriamiento y se analizó la correspondencia de los valores con los resultados obtenidos al resolver analíticamente la ecuación diferencial correspondiente.

Isaac Newton observo que mientras mayor sea la temperatura de un cuerpo, más rápido tiende a enfriarse, en base a estas observaciones y a sus avances en el cálculo diferencial e integral dedujo la ley sobre el enfriamiento de los cuerpos que hoy lleva su nombre, según Barroso (2018) la ley de enfriamiento de Newton plantea lo siguiente:

La temperatura de un cuerpo cambia a una velocidad que es proporcional a la diferencia de las temperaturas entre el medio externo y el cuerpo. Suponiendo que la constante de proporcionalidad es la misma ya sea que la temperatura aumente o disminuya, entonces la ecuación diferencial de la ley de enfriamiento es:

Donde t representa el tiempo transcurrido, T la temperatura del cuerpo en un instante de tiempo, Tm la temperatura media del ambiente y k una constante de proporcionalidad. Para aplicar esta ley las temperaturas suelen ser medidas en grados Fahrenheit (°F).

En el presente estudio se recabaron una serie de datos experimentales y se aplicó esta ecuación diferencial con las condiciones de frontera obtenidas, el experimento consistió en medir la temperatura de un termómetro que se introduce en un refrigerador para luego colocarlo fuera del refrigerador a temperatura ambiente y observar como aumenta la temperatura en función del tiempo evaluando su correspondencia con los resultados obtenidos mediante la ley de enfriamiento de Newton.

Mediciones de la Temperatura en distintos instantes de tiempo

En primer lugar se midió la temperatura ambiental, luego se introdujo un termómetro en el congelador de un refrigerador midiéndose la temperatura en el interior, posteriormente se extrajo dicho termómetro y se midió la temperatura al transcurrir 2 y 3 minutos, estas mediciones fueron realizadas en la ciudad de Santa Ana de Coro Estado Falcón el día 04 de abril de 2018 a partir de las 3:50 pm, Los datos obtenidos se muestran en las siguientes imágenes.

---

Imagen N° 1 Temperatura ambiental antes de realizar el experimento 3:50:00 pm (86 °F). Fuente: Fotografía tomada por el autor del artículo

---

Imagen N° 2 Temperatura del termómetro en el instante en que es retirado del refrigerador 3:58:00 pm (18 °F). Fuente: Fotografía tomada por el autor del artículo

---

Imagen N° 3 Temperatura luego de 2 minutos de retirar el termómetro del refrigerador 4:00:00 pm (68 °F). Fuente: Fotografía tomada por el autor del artículo

---

Imagen N° 4 Temperatura luego de 3 minutos de retirar el termómetro del refrigerador 4:01:00 pm (76 °F). Fuente: Fotografía tomada por el autor del artículo

---

Análisis de los datos obtenidos (Ley de enfriamiento de Newton)

En base a los datos obtenidos se elaboró la siguiente tabla:

Tiempo (t)	Temperatura (T)
0 Seg	18 °F
120 Seg	68 °F
180 Seg	76 °F

Luego de recabar esta información se aplicó la ley de enfriamiento al caso de estudio en cuestión. La ley de enfriamiento de Newton se expresa como:

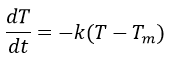
Al sustituir el valor de la temperatura ambiental (86 °F) se obtiene

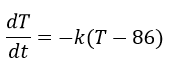
Esta ecuación diferencial es separable por lo que se resuelve colocando de un lado la variable correspondiente a la temperatura y del otro la correspondiente al tiempo e integrando ambos miembros:

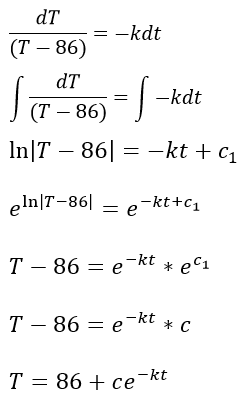
Esta solución posee dos constantes c y k cuyos valores se desconocen, por lo tanto se necesitan dos condiciones de frontera para poder encontrar los valores de c y k, estas condiciones vienen dadas por la temperatura en el instante inicial y la temperatura a los 2 minutos de haber sacado el termómetro del refrigerador.

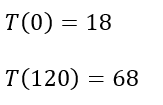
Sustituyendo la primera condición en la solución se obtiene

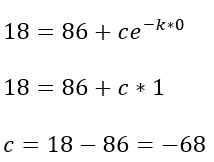
Ahora se sustituye el valor de c y la segunda condición en la solución

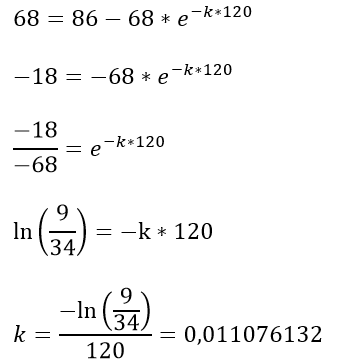
Con lo cual la solución particular de la ecuación diferencial planteada es

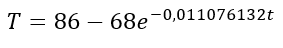
Si se sustituye en esta expresión t=180seg se obtiene

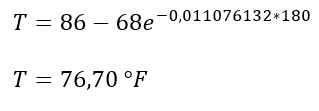
Lo cual corresponde aproximadamente con los datos obtenidos para el momento en que han transcurrido 3 minutos desde que se extrajo el termómetro del refrigerador según la imagen N° 4, se puede apreciar claramente que si t tiende a infinito se cumple que:

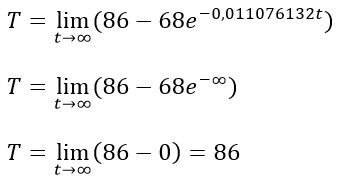
Lo cual coincide con la idea de que mientras más tiempo transcurra la temperatura del termómetro tenderá a igualarse con la temperatura ambiental.

CONCLUSIONES

1. Cuando el tiempo(t) tiende a infinito, la temperatura(T) tiende a igualarse con la temperatura media ambiental (Tm).

2. Para variaciones grandes de la temperatura la ley de enfriamiento de Newton no es precisa razón por la cual se aplican otros modelos que estudian el flujo del calor.